이번 포스트에서는 ‘블룸필터(BloomFilter)’의 개념과 특징을 알아보고 사용 예제를 통해 언제 어떻게 활용할 수 있는지 알아보겠다.
목차
블룸필터(Bloom Filter)
HBase, Redis 같은 고성능이 필요한 소프트웨어는 블룸필터(Bloom Filter)라는 자료구조를 사용한다. 블룸필터를 사용하면 불필요한 리소스 소모를 줄일 수 있어 소프트웨어의 전반적인 성능을 끌어 올릴 수 있다.
블룸필터는 집합 내에 특정 원소가 존재하는지를 확인할 수 있는 확률적인 자료구조다. 디스크 입출력이나 네트워크 통신 혹은 스핀락 같은 성능 저하를 유발시킬 수 있는 작업들 앞에 블룸필터를 추가해서 하지 않아도 되는 작업을 건너 뛸 수 있게 해주는 장치다.
블룸필터의 원리
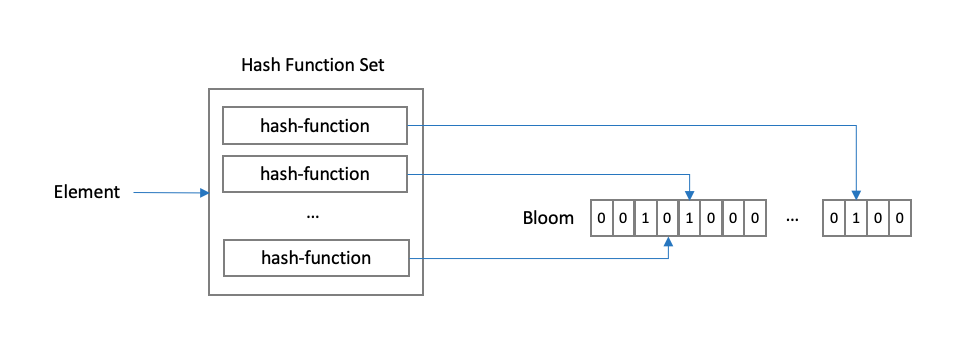
블룸필터의 동작 방식을 그림을 통해 확인해보자. 블룸필터는 Bloom이라는 비트맵과 해시함수들로 구성되어 있다.
우선 엘리먼트의 키 값을 해시함수에 적용해 해시 값을 얻어낸다. 얻어낸 해시 값을 이용해 모듈러 연산 등을 이용해 비트 위치를 특정하게 된다. 예를 들어 IP 주소를 해시 함수에 넘겨 해시 값을 얻어낸 후, 비트 개수로 모듈러 연산을 해서 비트 위치를 특정하게 된다.
일반적으로 블룸필터에서 해시 함수는 N개가 사용된다. 따라서 N개의 비트 위치가 특정된다.

엘리먼트가 추가되는 경우 특정된 위치의 비트를 1로 설정해준다. N개의 해시 함수가 사용되므로 N개의 비트가 켜진다.
엘리먼트 집합에 새로운 엘리먼트들이 추가될 때마다 이런 과정을 거치며 비트맵에 있는 비트들을 켠다.
엘리먼트가 집합에 존재하는지 확인할 때도 비슷한 과정을 거친다. 확인하고 싶은 엘리먼트에 해시 함수들을 적용해 비트의 위치를 특정한다.
특정된 위치에 있는 비트들이 모두 1로 켜져 있다면 집합에 존재할 수도 있다는 의미로 탐색과정을 거치면 된다. 반면 N개의 비트 중 하나라도 0으로 꺼져 있다면 집합에 엘리먼트가 존재하지 않는다는 의미다.
False Positive
블룸필터의 비트를 확인해서 모든 비트가 켜져있더라도 집합 내에 엘리먼트가 존재하지 않을 수 있다. 이는 해시 충돌(Hash Collision)과 비트맵의 크기 제약 때문이다.
해시 함수들은 본질적으로 해시 충돌이 발생할 수 있다. 서로 다른 키 값을 입력받았지만 동일한 해시 값을 리턴할 수 있기 때문에 다른 키 값이라도 같은 위치의 비트에 특정될 수 있다. 하지만 해시 충돌 확률은 매우 낮다.
비트맵의 사이즈 때문에 충돌이 발생할 수도 있다. 해시 함수로 얻어진 해시 값은 다르지만 이를 비트맵에 특정 시킬 때 충돌이 일어날 수 있다. 예를 들어 2와 10이라는 해시 값을 8비트 비트맵에 위치시키기 위해 8로 모듈러 연산을 하는 시나리오를 생각해보자. 2와 10을 8로 나눈 나머지는 모두 2다. 따라서 서로 다른 해시값인 2와 10은 모두 같은 위치의 비트에 접근하게 된다. 2라는 해시 값의 엘리먼트가 추가된 상태에서 10이라는 해시 값의 엘리먼트가 블룸필터 체크를 하면 존재할 수도 있다는 판단을 하게 된다. 물론 실제로 집합을 확인해보면 그런 엘리먼트는 없다.
이런 잘 못된 판단을 False Positive라고 한다. 잘못된(False) 존재(Positive) 판정이다. 블룸필터는 False Positive를 발생시키지만 False Negative는 발생시키지 않는다. 다시말하면 블룸필터에서 없다고 판단되면 진짜 없는 것이다.
False Positive 확률
당연한 말이지만 False Positive의 확률이 낮을수록 불필요한 작업을 안하기 때문에 성능이 좋아진다.
블룸필터의 False Positive 확률(p)은 블룸필터에 저장되는 엘리먼트의 개수(n), 비트맵의 사이즈(m), 해시 함수의 개수(k)에 따라 결정된다.

블룸필터에 설정되는 엘리먼트의 개수(n)가 늘어날수록 False Positive 확률은 올라간다. 엘리먼트 개수가 늘어날 수록 해시 충돌이나 같은 비트 위치에 특정되는 경우가 많아지기 때문이다.
비트맵의 크기(m)가 커질수록 False Positive 확률은 줄어든다. 서로 다른 해시 값이 같은 비트 위치에 특정되는 경우가 적어지기 때문이다.
엘리먼트의 키 값에 적용하는 해시 함수의 개수(k)가 늘어날 수록 False Positive 확률이 줄어들다가 최적값을 지나면 다시 증가한다.
False Positive 확률(p)과 엘리먼트 개수(n), 비트맵 사이즈(m)와 해시함수 개수(k) 사이에는 다음 공식이 적용된다.
n = ceil(m / (-k / log(1 - exp(log(p) / k))))
p = pow(1 - exp(-k / (m / n)), k)
m = ceil((n * log(p)) / log(1 / pow(2, log(2))));
k = round((m / n) * log(2));
https://hur.st/bloomfilter 사이트에 가보면 특정 조건이 고정되었을 때 최적의 나머지 값들을 계산해볼 수 있다. HBase 등에서도 이 공식을 이용해 최적의 값을 계산해 사용한다.
예제 - Guava BloomFilter
Guava 라이브러리를 이용해 블룸필터 예제를 작성해보자. Guava 라이브러리를 사용하기 위해 메이븐 의존성을 추가해줘야한다.
<dependency>
<groupId>com.google.guava</groupId>
<artifactId>guava</artifactId>
<version>32.0.0-jre</version>
</dependency>Guava 라이브러리의 BloomFilter 클래스는 다음과 같이 생성할 수 있다.
float errorRate = 0.1f;
int expectedNum = 500;
BloomFilter<Integer> bf = BloomFilter.create(Funnels.integerFunnel(), expectedNum, errorRate);BloomFilter.create()라는 정적 메소드에 사용할 것으로 예상되는 엘리먼트의 개수와 허용할 False Positive 확률을 넘겨준다. 그러면 라이브러리 안쪽에서 적당한 해시 함수 개수와 비트맵 사이즈를 계산해 최적화된 수치로 블룸필터를 만들어 준다.
BloomFilter의 put() 메소드를 통해 블룸필터에 엘리먼트를 설정할 수 있다.
bf.put(10);
bf.put(20);
bf.put(30);BloomFilter 클래스의 mightContain() 메소드를 이용해 비트맵이 설정되어 있는지 확인할 수 있다. 메소드에서 알 수 있듯이 존재할 수도 있음을 의미한다.
if (bf.mightContain(i)) {
// mightContain Element
} else {
// Element not contained
}이 메소드를 이용해 다음 예제를 구현해볼 수 있다.
float errorRate = 0.1f;
int expectedNum = 500;
Set<Integer> set = new HashSet<>();
BloomFilter<Integer> bf = BloomFilter.create(Funnels.integerFunnel(), expectedNum, errorRate);
for (int i = 0; i < 1000; i = i + 2) {
bf.put(i);
set.add(i);
}
int hit = 0;
int falsePositive = 0;
for (int i = 0; i < 1000; i++) {
if (bf.mightContain(i)) {
// Thread.sleep(1000L);
if (set.contains(i)) {
hit++;
} else {
falsePositive++;
}
}
}
System.out.println(hit);
System.out.println(falsePositive);0부터 999까지 숫자 중 짝수만 포함하도록 블룸 필터를 설정한다. 이후 0부터 999까지 모든 숫자에 대해서 블룸필터가 설정되었는지 확인한 후 설정되었다면 실제 HashSet을 열어서 엘리먼트가 존재하는지 확인한다. 만약 블룸필터를 통과했는데 HashSet에 없었다면 FalsePositive 케이스다.
위 예제 코드를 실행한 결과는 다음과 같다.
500
420부터 999중에 542개의 숫자가 비트맵을 통과했고, 그 중 42개의 False Positive가 확인되었다. BloomFilter를 생성할 때 넘겨주었던 Error Rate 값이 0.1f이었기 때문에 대충 500개 중 10%인 50개 정도는 False Positive가 발생할 것으로 예상했었는데 비슷한 수치가 나왔다.
Guava 코드를 열어보면 다음 코드로 최적값을 계산한다.
static int optimalNumOfHashFunctions(long n, long m) {
// (m / n) * log(2), but avoid truncation due to division!
return Math.max(1, (int) Math.round((double) m / n * Math.log(2)));
}
static long optimalNumOfBits(long n, double p) {
if (p == 0) {
p = Double.MIN_VALUE;
}
return (long) (-n * Math.log(p) / (Math.log(2) * Math.log(2)));
}위에서 봤던 식이 코드로 구현되어 있음을 확인할 수 있다.
만약 예상했던 엘리먼트의 개수를 훨씬 초과해서 블룸필터 설정을 한다면 False Positive 확률은 급증하게 된다. 예를 들어 50개만 사용될 것으로 예상되었지만 500개의 엘리먼트가 추가되었다면? 위 코드에서 expectNum 값을 50으로 바꾸고 실행하면 다음 결과를 얻게 된다.
500
500블룸필터의 비트가 지나치게 많이 켜져 있어 사실상 블룸필터 효과를 잃어버렸다.
이처럼 블룸필터를 사용할 때 내부 작동원리를 이해하고 적당한 값으로 생성해 사용해야 효과를 볼 수 있다.

댓글